Úhel je to, co nám vznikne, třeba když otevřeme nůžky. Roztáhneš nůžky víc a máš větší úhel, roztáhneš je méně a máš menší úhel. Zavřeš nůžky úplně a nemáš žádný úhel, jinak řečeno máš úhel nula.
Každé dvě tyčky z kterých uděláš stříšku svírají nějaký úhel. Je-li ta střecha ostrá pak jde o ostrý úhel. Je-li ta střecha tupá, pak jde o tupý úhel. A když nevíš (např roh papíru), pak jde o pravý úhel 🙂 Zatímco ostrých a tupých úhlu je mnoho, pravý je jen jeden. Ten který nám vznikne rozdělíme-li kruh na čtyři stejné části.
Jednotky úhlu
A když už umíme úhly porovnávat (ostrý úhel je menší než tupý, pravý úhel je větší než ostrý), jsme jen krůček od toho, abychom úhly očíslovali a měřili. Podobně jako jiné veličiny (třeba vzdálenost, tlak) mají i úhly různé jednotky v kterých se měří. Pojďme se na ně mrknout.
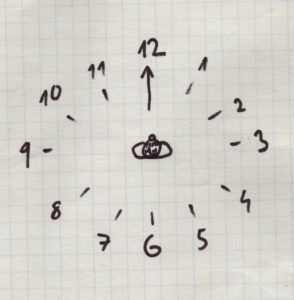HODINY – hodinové ručičky neustále svírají nějaký úhel. Hodinové ciferníky navíc každý zná a jsou všude na světě stejné (doufám O:). Popsat pomocí hodin úhel je snadné a srozumitelné. V praxi se tato jednotka používá hlavně na popsání směru. Kdy se tím myslí, že stojíš uprostřed pomyslného ciferníku, koukáš na 12 hodin a máš se otočit na jinou hodinu (viz. obrázek vpravo).
Například:
„Podívej, na třech hodinách je pěkný kostel.“ – upozornění, že napravo je pěkný kostel.
„Pozor, zuřivý pes na osmi hodinách!“ – zleva se za tebou žene pes.
STUPNĚ – stupně jsou nejpoužívanější úhlovou jednotkou a značí se malým kroužkem °. Zatímco předchozí hodiny dělí ciferník jen na 12 hodin. Stupně rozdělují kruh na 360°. Ve stupních můžeme tedy vyjádřit úhel mnohem přesněji. Pravý úhel, tedy čtvrt kruhu je 360°/4 = 90°. Vpravo vidíme úhloměr, speciální ohnuté pravítko na měření úhlů. A dole vidíte, že bez znalosti úhlů si už ani neotevřete dveře 🙂
-
Zdroj: wikipedie.org RADIÁNY – jsou odvozené od obvodu kruhu. K vyjádření úhlu požívají délku, oblouku jednotkové kružnice. Jednodušeji řečeno dělí kruh na 6,28 dílku. Proč 6,28? Pěkně je to znázorněno na animaci vpravo. Tato jednotka se používá hlavně u goniometrie (sinus, cosinus a tak). Dlouho jsem si myslela, že jednotkami radiánu je Π (pí). Ale není tomu tak. Π je jen řecké písmeno za kterým se schovává ošklivé číslo 3,1415926535…, zkráceně 3,14. Jednotka radiánu je rad, ale často se na ní zapomíná.
Celý kruh 360°= 2Π rad. Souvisí to s obvodem kruhu.
Půlkruh 180° = 2Π/2 = Π rad. Pokud ti to Π vadí, klidně místo něj napiš 3,14 rad.
Pravý úhel 90°= Π/2 rad.
- PROCENTA – je to divné, ale procenta se používají i k vyjádření úhlu. Konkrétně pak k
Dopravní značka určení strmosti silnice. Prudké klesání nebo stoupání je na silnicích označeno značkou např. 12%. Čím větší procento tím větší stoupák/padák. Desetiprocentním stoupáním je myšleno tak, že na 100m vystoupáme 10m výškových. Proč 10m? Protože 10m je 10% ze 100m. O jak prudký svah jde vidíme na obrázku níže.
Více o těchto podivných úhlových jednotkách se dočteš v článku o vrstevnicích. - GRADIÁNY – podobné jako stupně, jen dělí pravý úhel na 100 dílků. S touto jednotkou jsem se však nikdy nesetkala.
Jak převádět úhly
Kromě procent se dají všechny jednotky úhlů jednoduše převádět. Asi nejčastěji je třeba převádět stupně na radiány a naopak. I když to vypadá složitě, nejde o nic jiného než o trojčlenku. Furt vám to říkám, že trojčlenka si poradí skoro se vším. Když víš že plný úhel (celé kolco) je 2Π rad = 360° trojčlenkou dopočítáš co potřebuješ.
Př. 1: Převeď stupně na radiány
pravý úhel (90°), 180°, 30°, 45°, 120°
360° …. 2Π rad
90° ….. x rad
———————–
360/90 = 2Π/x ?
36/9 = 2Π/x ?
4 = 2Π/x ?
x = 2Π/4 ?
x = Π/2 ?
90° = Π/2 rad = 1,57 rad
PROCVIČ SI PŘEVÁDĚNÍ ÚHLŮ V TÉTO HŘE
K čemu jsou dobré úhly?
K čemu jsou úhly dobré? Třeba aby jsme si uměli nakrájet koláč. Úhly potřebujeme znát k vyjádření směru. A jelikož většina fyzikálních vlastností je vektorových tedy směrových, budou se nám hodit ve fyzice. Úhly potřebujeme ve stavebnictví, zkus postavit třeba jen domeček z papíru, bez pravého úhlu to bude pěkně šišaté. Vlastně všude kde se něco vyrábí, řeže, ohýbá, je třeba znát úhly. Každý materiál se sesypává pod jiným sklonem (úhlem) a s tím je třeba počítat, při stavbě cest a vytváření násypů. Zkus si vyrobit třeba jen obyčejný rámeček z papíru. Ustřihni si dlouhý pás papíru jako desku. A pak ji nařezej tak, aby se z ní dal poskládat rámeček, který se bude v rozích sbíhal stejně pěkně jako na obrázku vpravo.