Pravděpodobnost

Pravděpodobnost, že mě trefí meteorid je menší, než že dostanu ve škole pětku. Intuitivně umíme pravděpodobnost porovnávat, pojďme se jí naučit vyčíslit.

Co je to pravděpodobnost?

Pravděpodobnost možná chápeme jako nějaký pocit, že se něco stane. Jsme-li na poušti, můžeme prohlásit, že zítra bude pravděpodobně slunečno. Vidíme-li někoho bledého, slunit se několik hodin na přímém slunci, pravděpodobně se spálí. Použijeme-li ve svých tvrzeních slovo pravděpodobně, připoušítme, že jsme omylní. Omylní jsme sice všichni, ale jen ti opravdu moudří jsou si toho vědomi. Třeba takový Sokrates prohlásil: „Vím, že nic nevím.“ A ten toho věděl víc, než my všichni dohromady. Ale zpátky k pravděpodobnosti.

Pravděpodobnost nemusíme jenom intuitivně tušit, můžeme jí vyčíslit. Pravděpodobnost z hlediska matematiky je tedy číslo. Číslo které nám říká, jak moc se něco stane. Pravděpodobnost můžeme vyjádřit zlomkem, v procenty, nebo v desetinným číslem. Jak vidíš vpravo, všechno to spolu souvisí (viz.obr.2).

Pravděpodobnost = 1 = 100% je jistota.

Pravděpodobnost = 0 = 0% znamená, že k jevu nemůže dojít.

P = 0,5 = 50% je buď a nebo, padesát na padesát, například hod mincí.

Pravděpodobnost nemůže být větší než 100% neboli 1.

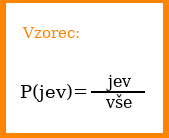
Jak jsme řekli v úvodu této kapitolky, pravděpodobnost se váže k nějaké události (jevu). Pravděpodobnost 0,2 sama o sobě nic neznamená. Musíme říct, čeho je to pravděpodobnost. Třeba toho, že budu zítra zkoušená před tabulí. Pravděpodobnost značíme takto:

P(jev) = číslo

Př.1:

P (hodím na minci lva) = 0,5

P(bude pršet na poušti v Kalahari) = 0,13 = 13%

P(bude dnes pršet u nás) = 40%

A teď jak jsem k těm číslům došla.

Jak se počítá pravděpodobnost?

Počítání pravděpodobnosti je celkem sranda, protože si při tom vyhrajeme. Začněme klasicky s hrací koustkou.

Pravděpodobnost teoreticky

Hrací kostka má šest stran a na každé straně je číslo (1,2,3,4,5,6). Jiné čísla tam nejsou.

Př.2: Hrací kostka
P(padne 7) = ?     Jaká je pravděpodobnost, že na kostce hodím sedmičku?
P(padne 1,2,3,4,5,6) = ?    Jaká je pravděpodobnost, že na kostce padne jedno z čísel 1 až 6?
P(padne 3) = ? Jaká je pravděpodobnost, že na kostce padne právě trojka a nic jiného?

Abychom spočítali pravděpodobnost, musíme zjistit všechny situace, které mohou nastat. V případě kostky jsou to tyto situace:

1. padne jednička
2. padne dvojka
3. padne trojka
4. padne čtyřka
5. padne pěta
6. padne šestka

Dohromady jde o 6 možných situací. A to,že padne šestka, je jen jedna z těchto šesti situací.

P(padne trojka) = 1 / 6 = 0,167 = 16,7 %
P(padne 7) = 0 / 6 = 0 = 0 %
P(padne číslo 1 až 6) = 6 / 6 = 1 = 100%
P(padne dvojka) = 1 / 6 = 0,167 = 16,7 %
P(padne sudé) = 3 / 6 = 0,5 = 50 %       Sudé čísla jsou na kostce tři (2,4,6). Šance že jedno z nich padne je 2 ku 6
P(padne liché) = 3 / 6 = 0,5 = 50 %

Oproti kostce má mince jen dvě strany, na jedné je lev a na druhé koruna. Všeho všudy jen dvě možnosti. Pravděpodobnost, že padne lev je jedna ku dvěma.

Př.3: Mince

P (padne lev) = 1 / 2 = 0.5 = 50%
P (padne koruna) = 1 / 2 = 0.5 = 50%

Tolik teorie. Ale jak je to ve skutečnosti? Co když zůstane mince stát na hraně? Nebo je kostka nevyvážená a padají samé šestky? Výše zmíněné výpočty jsou teoretické, počítají s vyváženou kostkou nebo minci. Pojďme teď zjistit, jak je na tom právě ta tvá kostka.

Pravděpodobnost v praxi

Abychom zjistili jak spravedlivou máme hrací kostku, musíme to vyzkoušet. Vezmeme tedy hrací kostku a házíme a házíme a házíme a házíme a…. a jednotlivé hody zapisujeme. Nemáte-li po ruce skutečnou hrací kostku, můžete jako já v př.3 použít tuto online kostku.

Př.4: Pravděpodobnost v praxi

Ze záznamu (vpravo) je na první pohled patrné, že online koskta není moc dobře vyvážena a šestkám příliš  neholduje. Ze 120 pokusů, padla šestka pouze 12 krát. Teoreticky by mělo být ve všech řádcích zhruba stejný počet čárek, ale v praxi tomu tak není. Pravděpodobnost, že padne šestka na této konkrétní nedokonalé online kostce je 12 ku 120 (12 hozených šestek ze všech 120 hodů).

P(padne 6 na online kostce) = 12 / 120 = 1 / 10 =  0.1 = 10 %
P(padne 5 na o.k.) = 16 / 120 = 2 / 15 = 0.133 = 13.3 %
P(padne 4 na o.k.) = ?
P(padne 3 na o.k.) = ?
P(padne 2 na o.k.) = ?
P(padne 1 na o.k.) = ?

Spočítáme-li pravděpodobnosti všech možných jevů, součet musí být 1 (neboli 100%). Toho můžeme využít ke zpětné kontrole.

No a tady jsem narazila na apku, kde si to můžete jednoduše odklikat:geogebra.org

Jaké asi bude počasí?

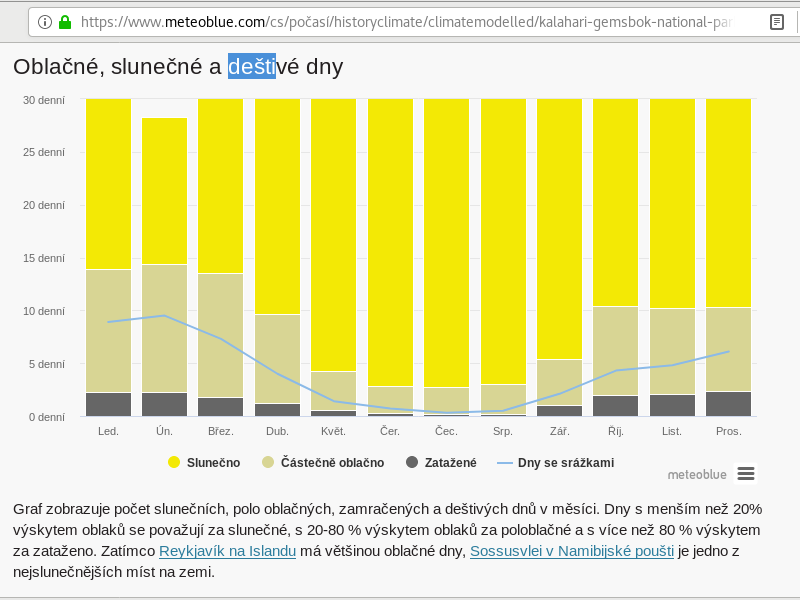
Pojďme ještě trochu poklábosit o počasí. Mám pocit, že vám dlužím vysvětlení, kterak jsem k číslu 13% došla (viz. př.1). Jo, i mě to příjde dost veliká pravděpodobnost na to, že by mělo v poušti pršet… Na rozdíl od kostky se počasím špatně hází. A pokud si člověk sám nedělá meteorlogické záznamy, musí se spolehnout na statistiky druhých. A tak jsem z grafu níže (modrá linka) nasčítala za celý rok deštivé dny v pošti Kalahari (asi 50 dní). Všech dní v roce je 365, takže pravděpodobnost, že zítra v Kalahari sprchne je 50 ku 365:

P(zitra zaprší) = 50 / 365 = 10 / 73 = 0.137 = 13,7 %. Přičemž zde nezohledňuji aktuální měsíc. Pokud je zrovna únor, je pravděpodobnost deště jistě vyšší než v létě. Dokážeš říc jaká?

P(zítra v Kalahari zaprší, je únor) = ?

P(zítra v Kalahari zaprší, je červen) = ?

K čemu je dobrá pravděpodobnost?

Umět pravděpodobnost je velmi užitečná věc. Na pravděpodobnosti jsou založená kasína, sázkové společnosti, ale třeba i pojišťovny a jejich majitelům se znalost pravděpodobnosti značně vyplatila. Ale i obyčejnému člověku, který netouží pravděpodobnost zpeněžit, to značně ulehčí život. Celý život se musíme o něčem rozhodovat. Ať už jde o rozhodnutí ve hře (kterou kartu mám táhnout), ve škole (učit se či neučit se? Jaká je šance, že učitel vyzkouší zrovna mě? Jaká je pravděpodobnost, že se zeptá zrovna na tuhle blbou otázku?), nebo o zdraví (Jít na operaci? Vzít si lék s takovými riziky?), pravděpodobnost nám s rozhodováním vždy pomůže.

Parádní film Enigma vypráví skutečný příběh o tom, jak jeden matematik i díky pravděpodobnosti vyhrál druhou světovou.

Pravděpodobnost ve hrách

Na téma pravděpodobnosti mě přivedla sympatická děcká hra – Na drátě. Oboustranné kartičky mají na druhé straně buďto ptáky stejné barvy, nebo ptáky stejného počtu, ale více o tom v odkazu.

Samozřejmě s pravděpodobnosti můžeme vesele počítat u karetních her a mnoha dalších.

Jak hrát, nebo naopak vyvážit hru aby byla spravedlivá pro všechny, tak tomu se věnuje obor zvaný teorie her.

Více o pravděpodobnosti

Na webu geogebra.org/t/probability jsem narazila na zajímavé aplikace týkající se pravděpodobnosti. Takže můžete prozkoumat, proklikat.