Závorky v matematice se používají proto, abychom určili pořadí v jakém se má provádět výpočet.
Co se počítá dřív?
Zkus vypočítat následující (hvězdička znamená krát) příklad 1:
3 + 4 * 2 = ?
Kolik ti vyšlo?
Ten, kdo to bude počítat zleva doprava (tak jak se to čte), dojde k výsledku 14. Protože 3 + 4 je 7. No a 7*2 je 14.
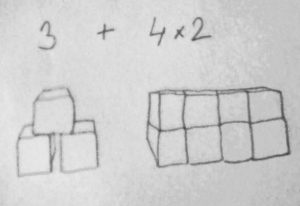
Ten, kdo si ale představí zeď z kostek (jak jsme si vysvětlovali u násobení) vyjde mu 11. Protože 2 kostky vysoká 4 kostky široká zeď obsahuje 8 kostek a k tomu přičtu 3, že.
Tak 14 nebo 11?
Správně je 11. Protože násobení má přednost před sčítáním. Tedy abychom byli přesní, násobení a dělení má přednost před sčítáním a odčítáním. Takže nezapomeň na to že počítá se jinak než se čte.
No a pokud potřebujeme zapsat příklad tak, aby mělo sčítání přednost, použijeme závorky. Například při řešení příkladu číslo 2.
Příklad 2: Do družiny chodí tři chlapci a čtyři děvčata. Kolik bonbonu musí družinářka koupit, aby dala každému dítěti dva bonbony?

Nejdříve sečteme děti a až pak každému přiřadíme bonbony. Nejdříve budeme sčítat a pak násobit. Sčítání tedy dáme do závorek.
(3 + 4) * 2 = 7 * 2 = 14
A nebo… nebo můžeme přiřadit dva bonbony klukům a dva bonbony holkám a pak všechny ty bonbony posčítat. Tři kluci po dvou bonbonech a čtyři holky po dvou bonbonech. Matematicky zapsáno takto:
 3*2 + 4*2 = 6 + 8 = 14
3*2 + 4*2 = 6 + 8 = 14
Vyšlo to stejně. Náhoda či pravidlo? Zkus poměnit počty holek a kluků a vyzkoušet tento příklad s různými čísly. Pokud ti to vychází vždy stejně, objevili jsme nové pravidlo. Pravidlo že
(3+4) * 2 = 3*2 + 4*2
Tomuto pravidlu se říká roznásobování závorek nebo vytýkání. Záleží na tom, z které strany se na to díváme. Zda se závorky zbavujeme, nebo ji vytváříme.
Roznásobili jsme : (3 + 4) * 2 = 3*2 + 4*2
Vytknuli jsme dvojku : 6 + 8 = 3*2 + 4*2 = 2 * (3+4)
Shrnutí
- Obsahuje-li příklad více různých znamének, pak nejdříve násobíme a dělíme a až pak sčítáme a odčítáme.
10+3*2+4/2-1 = 10+6+2-1 = 17 - Obsahuje-li příklad závorky, pak ze všeho nejdříve spočítáme to co je uvnitř závorek.
10+3*(2+4)/2-1 = 10+3*6/2-1 = 10+9-1 = 18 - Z předchozích bodů plyne, že sice nemusíš, ale když ti to udělá radost, nebo když na bod 1 neustále zapomínáš, můžeš si dát do závorek veškeré násobení a dělení.
3*2+4*2-2*2 = (3*2)+(4*2)-(2*2)
- Závorek se můžeme jednoduše zbavit roznásobením. Více v článku Roznásobování prakticky.
(6+4)*2 = 6*2 + 4*2 = 12+8 = 20 - Opačná operace k roznásobování je vytýkání. Používá se zejména při vytýkání neznáme.
6*n-2*n = n*(6-2) = n*4 = 4n