Hustota

Takže už víme, že věci kolem nás mají nějaký objem, hmotnost, teplotu. Pojďme to teď všechno zamíchat a objevit hustotu.

Otázky k zamyšlení vyzkoušení

Př.1: Co je těžší?

• Čaj nebo med?
• Voda nebo olej?
• Plastelína nebo voda?
• Teplá voda nebo studená voda?
• Polystyrén nebo voda?

Nejdříve si typněte a pak své odpovědi důkladně zvažte. Nemáte-li doma váhu, snadná pomoc, váhu si lze jednoduše vyrobit.

Př.2: Co je těžší 1 kg polystyrenu, nebo 1 kg kamení?

Zvažte ještě odpověď, jinak snadno naletíte na starý chyták 😉 Pokud stále trváte na tom, že kilo kamení je těžší než kilo polystyrénu, pak se mýlíte. Kámen je sice těžší než polystyrén, ale 1kg polystyrénu, je stejně těžké jako 1kg kamení. Protože kilo je kilo. A všechno co váží jedno kilo je stejně těžké. Čím to, že nám polystyrén připadá lehčí než kámen? V čem to vězí? Napoví další příklad.

Př.3: Dokresli váhu tak, aby porovnávala polystyren s cihlami. Čeho je víc?

Př.4: Co na čem plave? Co je nahoře?

• Čaj nebo med?
• Voda nebo olej? Pro lepší viditelnost, je dobré si vodu obarvit.
• Plastelína nebo voda?
• Teplá voda nebo studená voda? Pro lepší viditelnost, je dobré si teplou vodu obarvit.
• Polystyrén nebo voda?

Souvisí nějak hmotnost materiálů, kterou jste zjišťovali v př.1 s plavbyschopností, kterou zkoumáte v př.4?

Př.5: Viktorovy pokusy

Není to těžší, je to hustější

Pokud jste dokázali porovnat váhu různých materiálu v př.1, pochopili jste zradu v př.2 a dokreslili jste hromadu polystyrenu a pár malých kamínku, teda cihličku v př.3. Pak rozumíte hustotě. Ono říct, že kámen je těžší než polystyren, není úplně pravda. Snadno vám dokážu, že kámen může být lehčí než polystyren. Vezmu obrovský kus polystyrenu a malý kamínek. Abychom mohli skutečně srovnat váhu (hmotnost) různých materiálů, musíme porovnávat vždy stejné množství (objem).

A pak můžeme s klidem říct, že sklenice (o objemu 2 dl)  polystyrenu je lehčí než sklenice (2dl) kamení. Jenže už nemluvíme jen o hmotnosti. Mluvíme  o hmotnosti objemu a tomu se říká hustota. Hustota je hmotnost na konkrétním objemu. A má tedy jednotku složenou z jednotky hmotnosti (kg) a jednotky objemu (m³). Značka, kterou se ve fyzice značí hustota, je zakroucená mikulášská hůl, které se říká „ró“. Tiskací pak vypadá takhle: ρ.

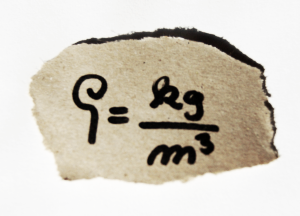
Odvodit si vzorec z jednotky je už snadné.

Př. 6: Která z látek má větší hustotu? Když víme že, sklenice s látkou_1 váží 80 g. A stejná sklenice naplněná látkou 2 váží 50 g. Skrytá odpověď.

Asi jste si pod slovem „hustota“ představovali něco jiného. Co je husté špatně se míchá, co je řídké dobře se míchá. Ale jak zamíchat šutr nebo polystyren? Ano, hustota se lépe představuje právě na kapalinách. Zkus si tedy ověřit, jestli to, co tu vyprávím, souhlasí s tím, co víš o míchání hustých věcí.

Př. 7: Vezmi si nějakou hustou tekutinu (sirup, med, těsto) a zkontroluj, zda skutečně váží při stejném objemu více než řídká tekutina (voda, olej).

Př. 8: Mám jablko a bramboru o stejné hmotnosti. Když jsem jej ponořila do odměrky, stoupla hladina o 300ml. Jablko má tedy objem 300ml (viz. pohádka O Archimedovi). Brambora oproti tomu vytlačila vodu jen o 100ml. Co má větší hustotu jablko či brambora?

Př. 9:  Jak velký bude kvádr zlata vážící 1kg?

ρ _zlata = 19 320 kg/m³
Ověřovací formulář (místo desetinné čárky použij tečku):

Hustota a plavání

V příkladu 4 jsme řešili, co na čem plave. Hodíme-li kus medu do čaje, potopí se na dno. Naopak nalijeme-li čaj do sklenice s medem, udělá loužičku na vrchu. Hustější med tedy zůstává dole, zatím co řidší čaj plave nahoře. Na obrázku vpravo zase vidíme ve sklenici s vodou kámen na dně a plovoucí polystyren nahoře. Jak jsme zjistili v předchozí kapitole, co se nám jeví těžší je ve skutečnosti hustější. Takže kámen s větší hustotou opět je opět dole, zatímco polystyren s nižší hustotou než má voda, plave nahoře.

Že to platí i v případě ruzně hustých tekutin, nám předvedl Viktor v př.5. Takže dokud nám někdo nedokáže opak, můžeme prohlásit, že vše co má nižší hustotu má tendenci plavat v tekutinách o vyšší hustotě.

Má to logiku, neboť co je těžší, je k zemi přitahováno větší silou (viz. Síla a hmotnost).

Př. 10:  Čím to, že lodě ze železa plavou?

Hustota a teplota

Jestli jste někdy začátkem léta plavali v jezeře, možná jste si všimli, že zvrchu je voda už pěkně nahřátá, ale když se potopíte hlouběji, je tam voda chladná. Že by jezero Slunce nahřálo jen z vrchu? Možná. A co pokus s horkou (žlutou) a studenou (modrou) vodou v následujícím videu?

Z videa je krásně patrné že horká voda má tendenci stoupat nahoru. Byla-li nahoře, vody se nepromíchaly, studená modrá zůstala dole a žlutá horká nahoře. Promíchala se jen slaba vrstva mezi vodami. Udělalo-li se to naopak, horká se snažila přes studenou dostat nahoru, čímž se obě vody promíchaly (žlutá+modrá=zelená).

Horká voda stoupá nahoru. Na tom principu je založeno i fungování radiátoru. Dole v kotelně se voda zahřeje a stoupá trubkami nahoru do radiátorů. tam se ochladí a klesá spodními trubkami zpět do kotelny, kde se zase zahřeje.

Jak je možné, že stejná látka má různou hustotu při různých teplotách? Už jsme si to naznačili, když jsme řešili teploměr. Zahříváme-li něco zvětšuje to svůj objem, nikoli však hmotnost.

Př. 11: Která hustota je větší?

kg/m³ => hmotnost/objem
studené:  10/1
teplé: 10/2 …zahřejeme-li studené, zvětší se objem (jmenovatel), ale hmotnost (čitatel) zůstane stejný
10/1 > 10/2
10 > 5
studené > teplé