Úvodní teorii o záporných číslech najdete zde. A tady rozcestník. V následující galerií řešených příkladu najdete ukázky různých výpočtů na:
Sama jsem si totiž včera uvědomila, jak důležité je pro mě vidět vyřešené příklady, když se snažím něco pochopit. Že mi to dá víc, než zdlouhavá teorie.
Sčítání a odčítání záporných čísel

 Když odčítám, pohybuji se na ose doleva. Když přičítám, pohybuji se na ose doprava. Pokud prodloužím osu do záporných čísel, můžu snadno počítat v záporných číslech.
Když odčítám, pohybuji se na ose doleva. Když přičítám, pohybuji se na ose doprava. Pokud prodloužím osu do záporných čísel, můžu snadno počítat v záporných číslech.
Tohle se dá pochopit celkem dobře.
Voprus začíná, když se do výpočtů začnou motat závorky a dvě znaménka po sobě… Ale žádný strachy i to se dá strávit.
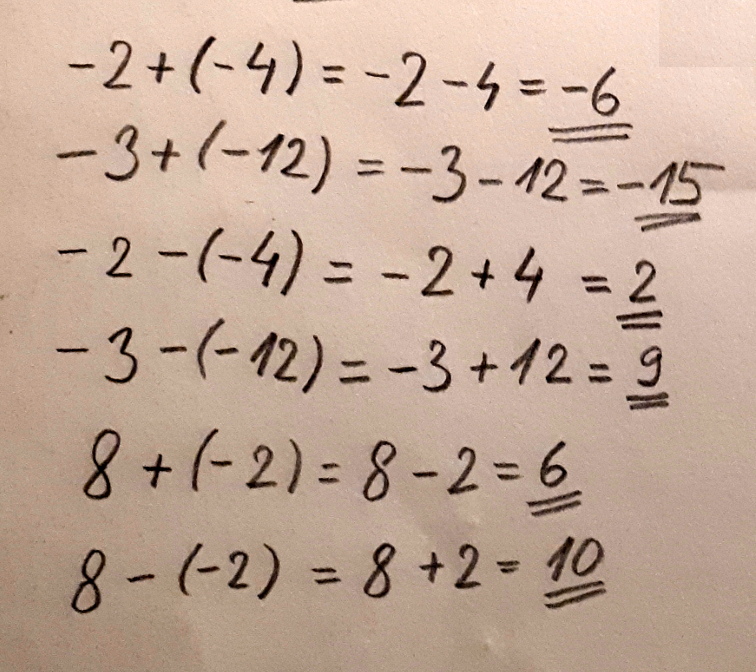
Já si představím pod zápornými čísly dluhy a pod kladnými čísly peníze.+(-4) přidávám do pokladničky 4korunový dluh, takže mi ubývá peněz a chudnu.-(-4) odebírám z pokladničky 4korunový dluh. Zbavuju se dluhu, takže mi přibývá peněz a bohatnu.

„No stejně jako se při odčítání větších kladných čísel od menších kladných dostaneš do záporu.“Pokud ti to hlava nebere, v klidu, zkusíme to ještě jinak.

 <- Čím větší číslo odčítám, tím menší výsledek získávám (viz. výpočet vlevo). A protože už víme, že nulou čísla nekončí, dostanu se do záporných čísel.
<- Čím větší číslo odčítám, tím menší výsledek získávám (viz. výpočet vlevo). A protože už víme, že nulou čísla nekončí, dostanu se do záporných čísel.
-> Vpravo zkouším opačný postup. Snižuji číslo, které odčítám a sleduji jak mi výsledek roste. A protože už vím, že čísla nulou nekončí, můžu odečíst číslo které je menší než nula a logicky by měl výsledek zase vzrůst.
Násobení a dělení záporných čísel

 <- Když se mi dluh zdvojnásobí, pak dlužím dvakrát víc.
<- Když se mi dluh zdvojnásobí, pak dlužím dvakrát víc.
-> Když mi někdo odpustí polovinu dluhu, pak mu budu dlužit dvakrát méně.
Všimněte si, že když 8:4=2, pak 8:2=4. Přehodím-li u dělení čísla sousedící s rovnítkem, platí to. No a když to platí u kladných, musí to platit i u záporných. Takže když -8:2=-4, pak musí platit -8:(-4) = 2.
Jiný princip, který musí být zachován najdeme i u násobení. Když 4 * 2 = 8 , pak 8 : 2 = 4. Takže když -8 : 4 = – 2, pak -8 : (-2) = 4.
Tak nějak matematici došli k pravidlu, že s násobením DVOU záporných čísel se dostávám s výsledkem do kladných. A to samé platí o dělení. Ale když je jen jedno záporné a druhé kladné, pak se furt motám v záporu.
A co když mám ty čísla TŘI a více?
Když nevím, převedu si to na něco, co vím – to je základní princip matematiky.
8 * (-4) : 2 = cislo : 2
cislo = 8 * (-4) = -32
cislo : 2 = -32 : 2 = -16
Ještě to zkusím jinak, ať se ujistím.
8 * (-4) : 2 = 8 * cislo
cislo = (-4) : 2 = -2
8 * cislo = 8 * (-2) = -16
To byla substituce. Kousek co mě děsil jsem si „přelepila“, bokem spočítala a výsledek na nálepku napsala. Tím jsem tři čísla zredukovala na dva, která spočítat umím. Více v článku Substituce.
Myšlenka tohoto příspěvku byla, rychle si proskroluji, dokud nenarazím na typ příkladu s kterým potřebuji pomoct. Buď to pochopím z ukázky, nebo si přečtu poznámku vedle obrázku. Tak snad se povedlo.