V tomto textu si vysvětlíme, jak se zlomky přehazují přes rovnáse a jak vytknout neznámou. V článku Trojčlenka a zlomky jsem prováděla se zlomky různé kejkle, které nemusejí být každému jasné. Rovněž při práci se vzorci potřebujeme umět vytýkat neznáme. Tak se teď na to mrkneme, ať v tom máme pěkně jasno.
Úpravy, které si teď popíšeme se týkají rovnice, která má na obou stranách rovnítka jen zlomky. Jak můžeme vidět v příkladu 1.
Př.1.: Čemu se rovnají neznámé a a b ? Nevíš-li, čti dál a k příkladu se pak vrať.
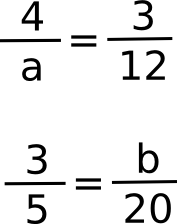
Takovéto rovnice získáme například z trojčlenky. Ale jak si prozradíme dále, můžeme do tohoto tvaru dostat v podstatě libovolnou rovnici.
Jak převést celé číslo na zlomek
Zlomek není nic jiného než dělení (viz. Zlomky a dělení), kde nahoře mám počet čokolád a dole počet mlsounů. A když jsem lakomec a všechny čokolády si chci nechat sama pro sebe, mezi kolik mlsounů je musím rozdělit? Ověř si svůj tip s pomocí kalkulačky. A zkontroluj, zda to sedí i pro různé počty čokolád viz. př.2:
Př.2.: Čím musím podělit číslo, aby mi zůstalo stejné číslo?
5/x = 5
8/x = 8
24/x = 24
155/x = 155
Přišli jste na to, čemu se rovná x? Jakým číslem můžeme vesele dělit a dělit, aniž by se cokoli změnilo? Ne, tak zkoušejte dál 😉 Pokud, už jste našli toto kouzelné číslo, pak jednoduše převedete rovnice z příkladu 3 do tvaru dvou zlomků, které jsme si ukázali v příkladu 1.
Př.3.: Upravte rovnice tak, aby obsahovali zlomek nalevo i napravo od rovnáse.

Jak dostat jmenovatele do čitatele
Co já vím? Třeba přehodíme čitatele a jmenovatele? To nezní moc přesvědčivě, co? Tak si to raději ověříme. Tak třeba na čísle 4:
 … čtyř se rovná čtyřem
… čtyř se rovná čtyřem
… rozdělím-li čtyři bonbony mezi jednoho (sebe :), budu mít čtyři bonbóny!
!!! přehodím čitatele jednoho zlomku a přestává to dávat smysl. Něco je zle!
Takže přehodit jen tak čitatele s jmenovatelem, kdykoli se mi zlíbí, nemohu. Protože jak vidíme výše, porušili bychom rovnost. Ale co když přetočím celou rovnici?
 I když je to podivná úprava a změnilo se mi množství, rovnost zůstala zachována. Stále mám na levé straně rovnice to samé co na pravé, takže rovnáse tam může zůstat. Zajímavé, že? Pro jistotu to vyzkoušej i s jinými čísly.
I když je to podivná úprava a změnilo se mi množství, rovnost zůstala zachována. Stále mám na levé straně rovnice to samé co na pravé, takže rovnáse tam může zůstat. Zajímavé, že? Pro jistotu to vyzkoušej i s jinými čísly.
Ono tahle podivuhodná úprava ti začne dávat smysl, když si trochu pohraješ s váhami. Představa rovnice jako vah je v tomto případě přímo spásna. Např. mám váhu v rovnovážném stavu v obou miskách mám 4 kulikčky. Co se stane když obsah jedné misky zdvojnásobím? No dojde k narušení rovnosti. Ale když zdvojnásobím obsah obou misek, s rovností se nic nestane. A stejně tak když srazím obsah obou misek na polovinu, rovnost zůstane zachována.
Př. 4.: Převrať oba zlomky rovnice a ověř zda zůstala rovnost zachována. Zda je napravo stejná hodnota jako nalevo. Použij klidně kalkulačku.
2/1 = 2/1
4/1 = 8/2
4/16 = 2/8
5/10 = 15/30
1/2 = 1/2
… vymysli si další
Přehazování čitatele a jmenovatele přes rovnáse
Takže už víme, že můžeme přehazovat čísla okolo zlomkových čar. Teď si prozradíme jak přehazovat čísla přes rovnáse. Jde v podstatě o podobný princip, jako když se sčítání promění za rovnítkem na odčítání. Tak stejně se dělení změní na násobení a násobení na dělení. Víc ti to bude jasné, když si pohraješ s Doplňovačkou znamének.
Jednodušeji řečeno: To co je dole, přeskočí rovnáse a dostane se nahoru. A to co je nahoře, se za za rovnítkem dostane do jmenovatele. A to je celá věda.

Takže vytknout a z rovnice v první příkladu by mohlo vypadat takto:


nebo takto:
Teď když už víš jak na to dopočítej neznáme z příkladů 1 a 3.